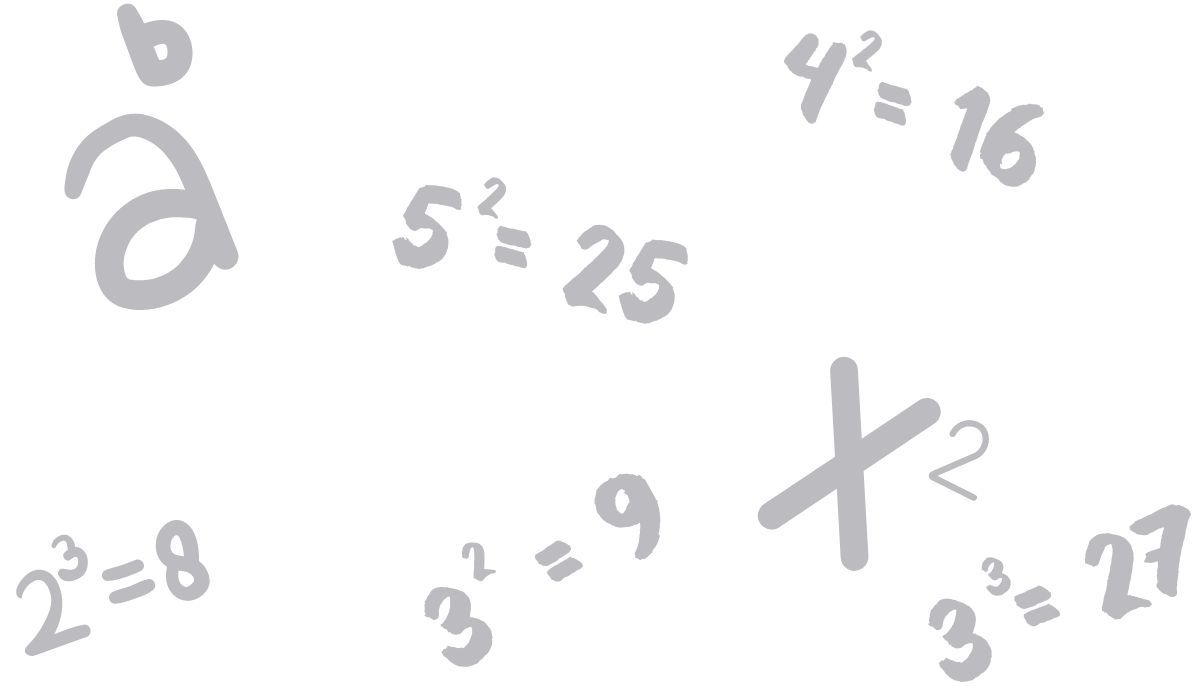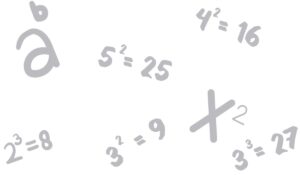Properties of Exponents and How to Use Them
Table of Contents
- Product Rule
- Quotient Rule
- Negative Power Rule
- Fractional Power Rule
- Powers of Products (and Quotients)
- Powers of Powers
- Zero Power Rule
What Are Exponents?
Exponents are a shorthand for showing repeated multiplication within math. For example, the number 24 is the same as writing out the expression 2 x 2 x 2 x 2. Both operations result in the answer 16. Likewise, if you did the operation 32, you would get the number 9 because 32 is the same as 3 x 3. A common mistake students make is confusing the exponent (the small number) with a number that should be multiplied by the base (the big number), doing 3 x 2 instead of 3 x 3. Remember that the exponent indicates how many times the base should be multiplied by itself. This becomes useful when using bigger numbers as you do not have to write 2 x 2 x 2 x 2….. repeatedly in order to represent that specific operation or another quantity. Instead, it can be neatly summed up with the exponent 24.
There are a couple of key rules when it comes to doing operations with exponents. In this article, we will discuss the rules you need to know below:
Product Rule
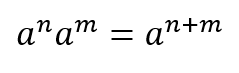
The first rule most students learn is the product rule. Illustrated above, this rule states that when you multiply exponents with the same base, you add the exponents together. That means that if you had the expression 32 x 33, the answer would be 35.
Remember that exponents symbolize repeated multiplication, so 32 is 3 x 3, and 33 is 3 x 3 x 3. Altogether, you have (3 x 3) x (3 x 3 x 3) or 3 times itself 5 times. That is why 32 x 33 equals 35 instead of 3 to the 6th power.
Quotient Rule
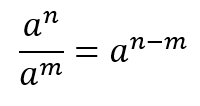
Opposite to the product rule, the quotient rule states that if you are dividing two quantities with the same base, you will subtract the exponents. 35/32 equals 33 because (3 x 3 x 3 x 3 x 3) divided by (3 x 3) means two of the five 3s will cancel each other out, leaving you with 33 as the result.
Negative Power Rule
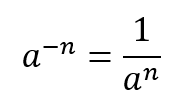
Similar to the product rule, a common mistake students make with the negative power rule is multiplying the exponent times the base, thinking that a negative power makes the answer negative. This is not the case. Negative exponents do not make the results negative. Instead, negative exponents turn the number into fraction. When you have a negative exponent, put the number 1 over the base and make the exponent positive. Then simplify the expression where necessary. 3-3 for example becomes 1/33 or 1/27.
Fractional Power Rule
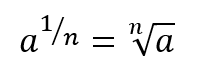
When the exponent itself is a fraction, the expression becomes a radical. The base goes inside the root symbol and the denominator of the fraction goes on the hook of the radical. If the numerator for the rational exponent is a number other than 1, it will go inside the root symbol with the base.
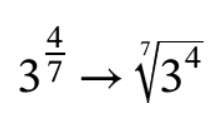
Powers of Products (and Quotients)
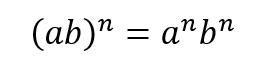
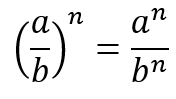
When you have an exponent on the outside of a set of parentheses, distribute the exponent to all terms inside. If you have (xy)3, it becomes (x3y3). If you have a fraction such as (2/3)2, it becomes (22/32) or 4/9.
Powers of Powers

Similarly to the rule above, distribute an exponent when it is on the outside of a set of parentheses. If there are already exponents inside the parentheses, multiply the exponents together (not add!).
Zero Power Rule
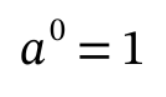
This might be the easiest rule of all the properties of exponents. Anything raised to the power of 0 is equal to 1.
30 = 1.
4250 = 1
1,625,3820 = 1
View our resources
Strive Resources | TpT | Made By Teachers | Classful | Etsy