Table of Contents

1. 3-4-5 Right Triangles
2. 30-60-90 Degree Right Triangles
3. 45-45-90 Degree Right Triangles
4. 5-12-13 Right Triangles

Special Right Triangles

When it comes time for students to prepare for standardized tests, they may start encountering something called special right triangles. “So what are they?” you may ask. Even though the name may sound a little fancy, the concept is quite simple. Special right triangles are right triangles with some regular features which makes calculations easier. By learning about these triangles and how to recognize them, students can save a lot of time running calculations for side or angle measurements when it comes to basic trigonometry. When it comes to test prep, 3 types of special right triangles are most common: 3-4-5 right triangles, 30-60-90 degree right triangles, and 45-45-90 degree right triangles. Below, we will cover what you need to know about these most common special right triangles, including one more you might need to know.

3-4-5 Right Triangles

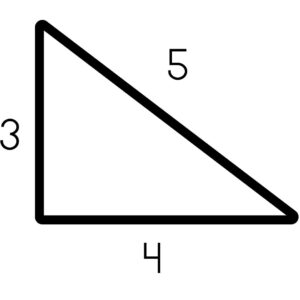
3-4-5 right triangles are some of the most common special right triangles students will see. They are so named because the ratio of their sides are always 3 – 4 – 5. The 3 and 4 always refer to the measurement of the legs, and the 5 refers to the measurement of hypotenuse. That means that if one leg has a measurement of 3 and the other leg has a measurement of 4, the hypotenuse must be 5. Likewise, if you were to have other measurements that match this ratio, you could figure out the remaining side. If the hypotenuse of a triangle measures 20 (5 x 4) and the leg measures 12 (3 x 4), it must be true that the remaining leg measures 16 (4 x 4).

Note in the parentheses that each of these side measurements still have the ratios of 3-4-5. In this example, though, each of these measurements have been multiplied by 4. Just like when you reduce a fraction or find a multiple of a number, if you change one part of this ratio, every other part must be changed in the same way. If two sides of a right triangle measure 12 and 9, the hypotenuse must be 15. This is because everything in the ratio 3-4-5 has been multiplied by 3. Simply identify whether you can divide the measurements given by the same number to see if it ends up giving you the ratio 3-4-5. By recognizing this relationship, you can avoid using the Pythagorean Theorem and save time.

30-60-90 Degree Right Triangles

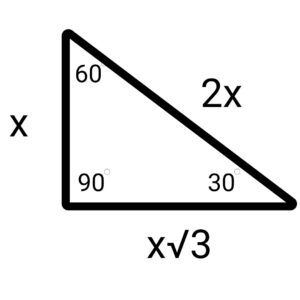
The second kind of special right triangle students should know is a 30-60-90 degree triangle. Like the name implies, this kind of right triangle has measurements of 30 degrees, 60 degrees, and 90 degrees respectively. An important note that you should be aware of is that the sides of a triangle will correspond to the angle that is opposite from it. That means that if 30 degrees is the smallest angle within the triangle, it will be opposite from the smallest side of that same triangle (labeled x in the diagram). Likewise, the 90 degree angle will be opposite from the largest side in that right triangle (labeled 2x), since it is the largest angle. The second largest angle, 60 degrees, is across from the second largest side (labeled x√3).

In practice, that means that if we can determine the angles of the right triangle to be in the ratio of 30-60-90, if the smallest side is 3, the second largest side will be 3√3, and the largest side, the hypotenuse, will be 6.

In a variation of this type of problem, you may be given the measurement of the second largest side instead. This makes things a little trickier because of the square root. To solve something like this, you should create an equation. Therefore, if we know the second side to equal 8, it must be equal to x√3. That means 8 = x√3, and we can solve this equation for x.

8 = x√3

Divide both sides by √3 to isolate the x.

8/√3 = x

Radicals cannot be in the denominator of a fraction, so we must multiply by √3 on the top and bottom

8(√3) / √3(√3) = x

This gives the result

(8√3) / 3 = x

So (8√3)/3 is the value for the smallest side.

45-45-90 Degree Right Triangles

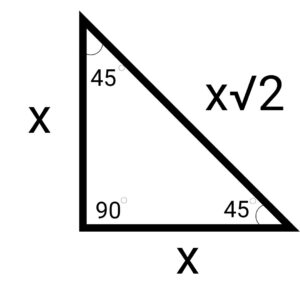
Similar to 30-60-90 degree right triangles, 45-45-90 degree right triangles also have a regular relationship between the angles and the side measurements. In this type of special right triangle, the measurements of both the legs are equal, and the measurement of the hypotenuse is equal to either of the legs times the square root of 2 (x√2). As before, the 45 degree angles will be across from the identical sides, and the 90 degree angle will be across from the hypotenuse. If one leg has a measurement of 4, the other leg will have the same measurement, and the hypotenuse will be 4√2. If the measurement of the hypotenuse is 10, we can construct an equation like above and solve for x.

10 = x√2

Divide both sides by √2

10/ (√2) = x

Multiply by √2 on the top and bottom of the fraction as radicals cannot be in the denominator.

10 (√2) / (√2)(√2) = x

Simplify

(10√2)/2 = x

5-12-13 Right Triangles

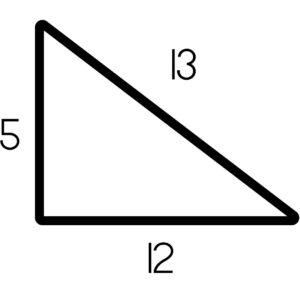
Similar to 3-4-5 right triangles, 5-12-13 right triangles have a ratio between the side measurements of 5 – 12 – 13. This ratio always remains the same regardless of how much larger or smaller the shape becomes. If the legs measure 10 (5 x 2) and 24 (12 x 2), the hypotenuse must be 26 (13 x 2). If the hypotenuse is 39 (13 x 3) and a leg is 15 (5 x 3), the remaining leg must be 36 (12 x 3). Simply identify whether you can divide the measurements given by the same number to see if it ends up giving you the ratio 5-12-13.

Special right triangles can help students save a lot of time. It is important to get familiar with the ratios and understand how each apply to these right triangles. Memorizing and recognizing them will enable you to solve problems much more quickly without resorting to using the Pythagorean Theorem and having to utilize a calculator or work things out by hand. When taking tests like the ACT and SAT, every second matters to your success. Mastering this concept can be a huge time saver and boost your score!

View our resources

Strive Resources | TpT | Made By Teachers | Classful | Etsy