Step by Step: How Do I Solve An Equation?
Have you tried solving an equation and ended up stuck on a step halfway through? Having trouble making sense of equations or why they matter? In each installment of Step by Step, we’ll explain how you can approach a variety of concepts more effectively. Equations are useful way of solving for an unknown amount when other information is present. As the name suggests, equations present two amounts that are supposed to be equal to each other. This is one of the first concepts students encounter in Algebra, but the key skills you learn here carry on to every level of math afterwards, making this is one of the most important skills to master.
The basics
So ultimately, what is the goal of solving an equation? Whenever you’re asked to solve, that means get the variable (the letter that stands in for an unknown number) by itself. So our goal is to move any other numbers (and maybe other variables) away from the variable we want to solve. Most equations will have only one variable present; after all, you can’t get a number as your answer if there’s another unknown amount present…but that discussion is for another time.

Since equations represent two equal amounts, think of them like a balancing scale. When solving the equation, we want both sides to represent the same amount all throughout the problem, so whenever you perform an action on one side of the equation, you must perform the same action on the other side of the equation. One method you can use to keep this in mind is to draw a line where the equal sign is in the equation. Whatever you do on one side of the line must be repeated on the other side.
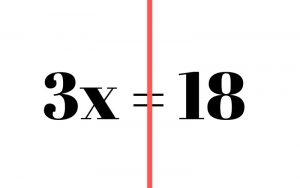
Solving One Step Equations
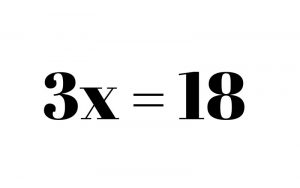
In one step equations, you only need to perform one operation in order to solve the problem. Let’s take the equation 3x = 18. On the left side, we have 3x, which means 3 times the unknown number x. In other words, 3 times an unknown number is equal to the number 18, which is on the right side of the equation.
Since our goal is to get the x by itself, we want to cancel out the 3 on the left side. To cancel out a number, you must do the opposite operation – in this case, division is the opposite of multiplication, so we divide by 3 on the left.
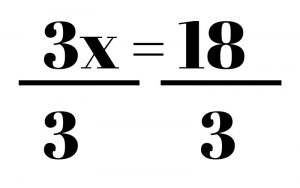
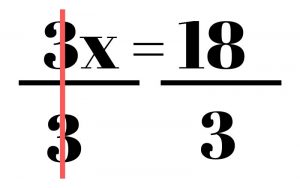
As we mentioned above, though, we must keep the equation equal at all times, so if we divide by 3 on the left side, we must divide by 3 on the right side. When you divide a number by itself, it cancels out and leaves us with 1, so we’re left with 1x on the left and 6 on the right.
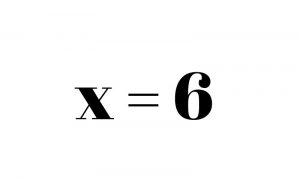
Solving Two Step Equations
Two step equations require two steps to solve the problem. They typically require you to both multiply/divide and add/subtract within the equation. When solving equations that require two steps or more, keep in mind that you will usually do the order of operations in reverse, at least for some of it. Remember PEMDAS stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction. In most numerical problems, you would start with parentheses and continue with the steps to the right. In equations, it’s the opposite, particularly with the MDAS part. You should still take care of anything in parentheses first, then exponents, but that applies more to multi-step equations. After that, though, you should move any numbers added or subtracted to your variable and then get rid of any multiplication or division, if applicable. Take the equation 4x – 2 = 14. We want to move the -2 first, so we do the opposite operation of addition.
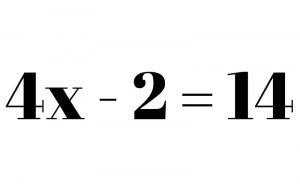
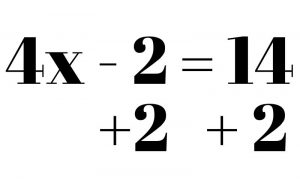
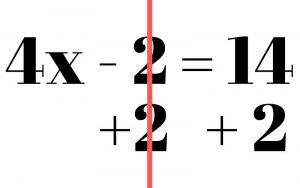
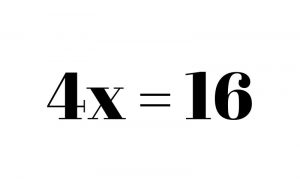
Once that’s done, we are left with 4x = 16. In order to get rid of the 4, which is multiplied times the x, we must divide. X = 4. Keep in mind that any numbers next to your variable (the 4 in this problem) should be the last thing that you touch in an equation. Everything else should be moved first.
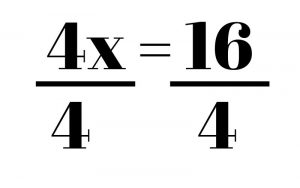
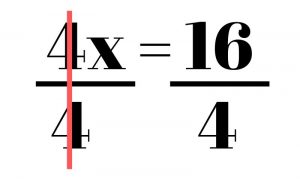
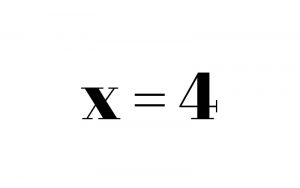
Solving Multi-Step Equations
Multi-step equations are like two step equations. These types of equations often have parentheses or fractions. You’ll want to distribute and handle any numbers inside the parentheses first; you should take care of exponents at this time too. The key things to remember are:
- Take these equations one step at a time, and write down each step. The more you try to do at once, the more likely you will make a mistake and forget something.
- Follow the same steps as two-step equations. Once you handle parentheses and exponents, start with any numbers that need to be added or subtracted.
So let’s work on the equation 3(2x + 4) = 36.
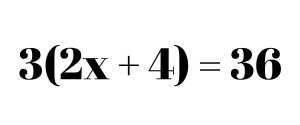
Whenever a number is written right next to a set of parentheses, it means multiply. So we start by distributing the 3 inside the parentheses.
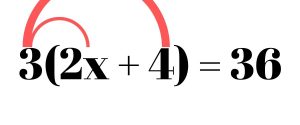
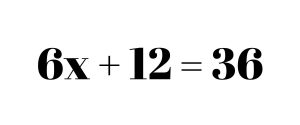
This leaves us with 6x + 12 = 36. Once we’re done distributing, we’re basically left with a two-step equation. Like above, we start by cancelling the addition, so we subtract 12 on both sides.
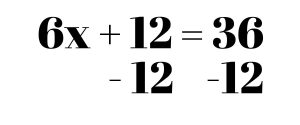
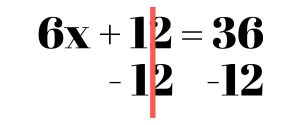
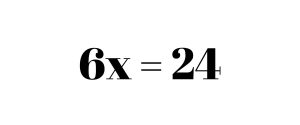
Now we have 6x = 24. To cancel out the 6, we divide by 6 on both sides. This leaves us with the answer x = 4.
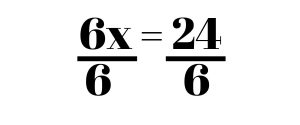
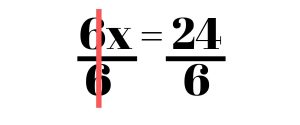
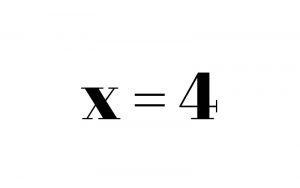
Looking for additional practice solving equations? Check out our Algebra worksheets! There are hundreds of problems to practice on, and we’re constantly adding more. If you still need help after some more practice, consider giving us a call and working with one of our Algebra tutors.
Looking for extra practice? Try our resources:
Related: Equations Mastery Pack
View our resources
Strive Resources | TpT | Made By Teachers | Classful | Etsy









